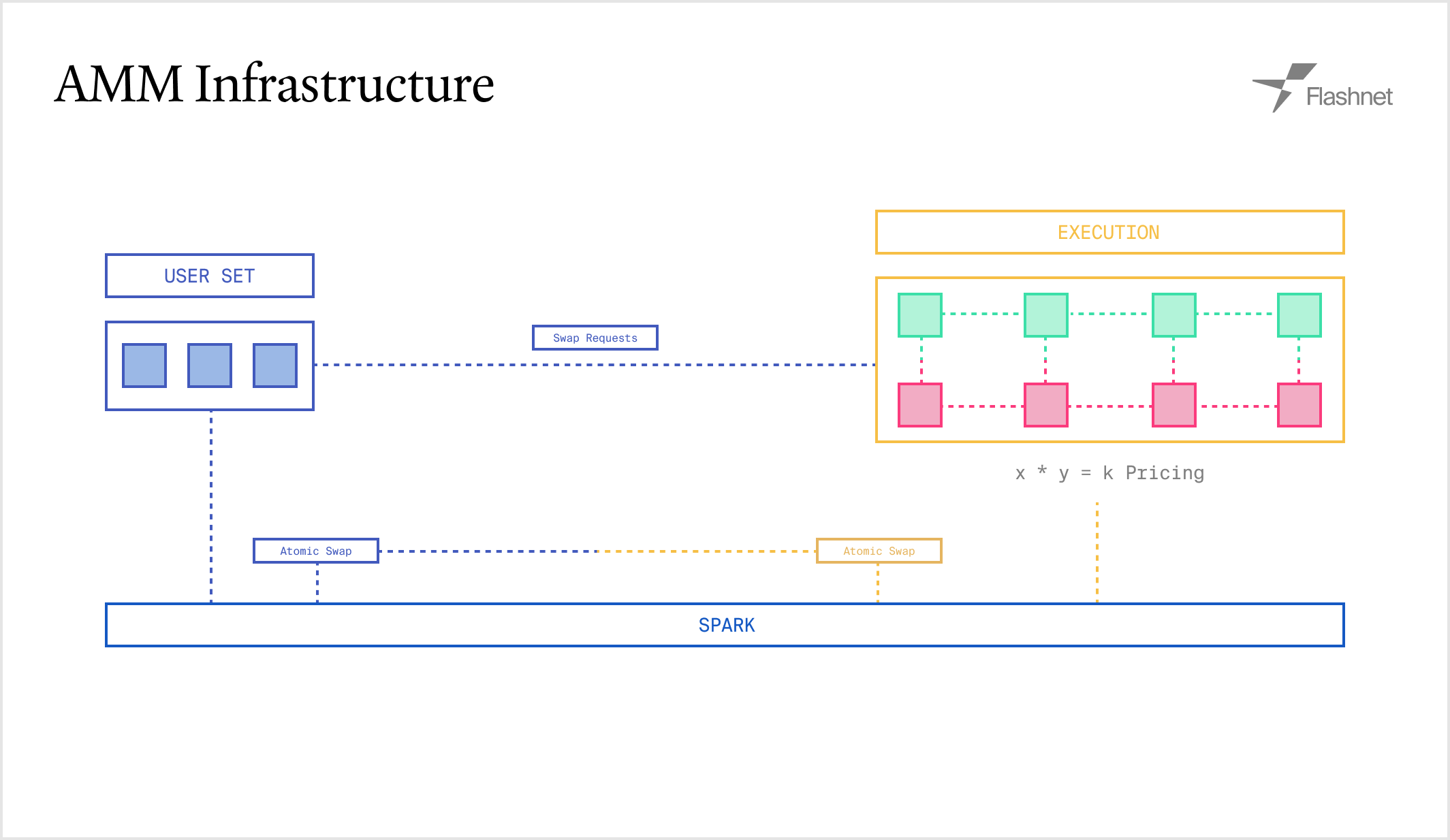
Flashnet AMM powers automated markets for the long-tail of assets, allowing its users to be passive liquidity providers and grow nascent markets. Flashnet AMMs can be either single sided or double sided. The liquidity for AMMs lives on the Flashnet settlement layer, which is secured by a set of validators and can only move with valid intent. When trading against the AMM, the flow follows the Flashnet Trade flow, with the exception that the AMM is used as the counterparty and no matching engine is required.

​
Constant Product AMM

The constant product AMM is a simple y * x = k curve that allows users to deposit two assets and enable them to be traded against each other. The price of the assets is determined by the ratio of the two assets in the pool. 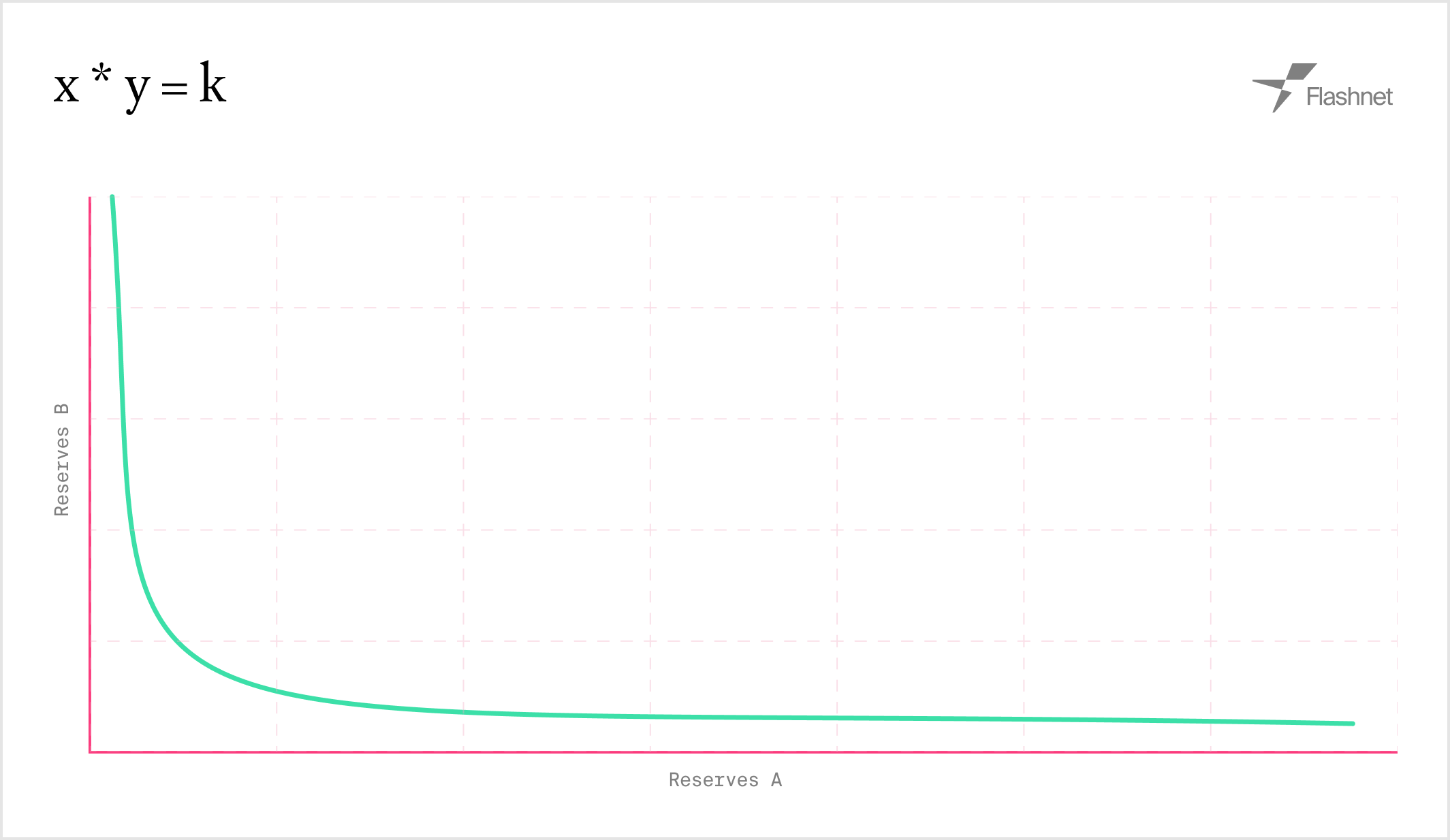The mathematical model follows:
  • Price(A) = Reserve_B / Reserve_A
  • Trade execution follows: (Reserve_A + ΔA - fees) * (Reserve_B - ΔB) = k where k is the constant product of the reserves.

​
Bonding Curve AMM (Single-Sided)

The single-sided AMM uses a bonding curve for gradual price discovery, making it ideal for launching new tokens. It allows a creator to supply tokens and define a price curve that evolves as the tokens are sold. Once a certain amount of the supply is sold, the pool “graduates” into a standard constant product AMM.

​
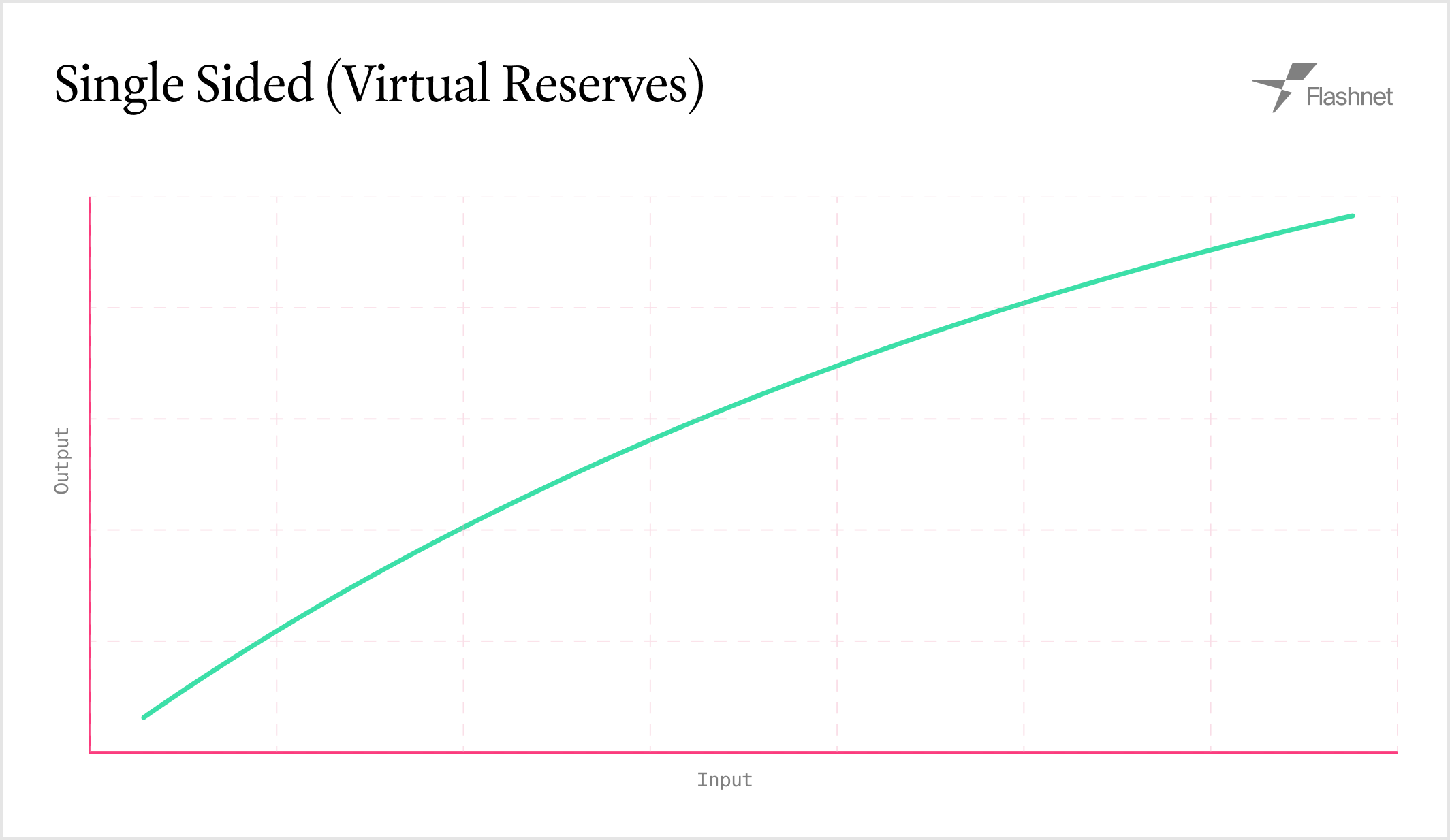
Price Mechanism

We model single‑sided sales with virtual reserves that sit on a constant‑product curve. Let initial virtual reserves be v_A^0 and v_B^0 with k_v = v_A^0 * v_B^0. As tokens are sold, we maintain:
  • current_v_a = v_A^0 - tokens_sold
  • current_v_b = v_B^0 + quote_raised
The instantaneous price is: P = current_v_b / current_v_a Swaps update virtual reserves using constant product math:
  • Buy A with B (B→A): new_v_b = current_v_b + ΔB, new_v_a = k_v / new_v_b, output ΔA = current_v_a - new_v_a.
  • Sell A for B (A→B): new_v_a = current_v_a + ΔA, new_v_b = k_v / new_v_a, output ΔB = current_v_b - new_v_b.

​
Concentrated Liquidity AMM

The concentrated liquidity AMM implementation allows liquidity providers to concentrate their capital within specific price ranges, similar to Uniswap V3. This enables more capital-efficient liquidity provision compared to traditional constant product AMMs. 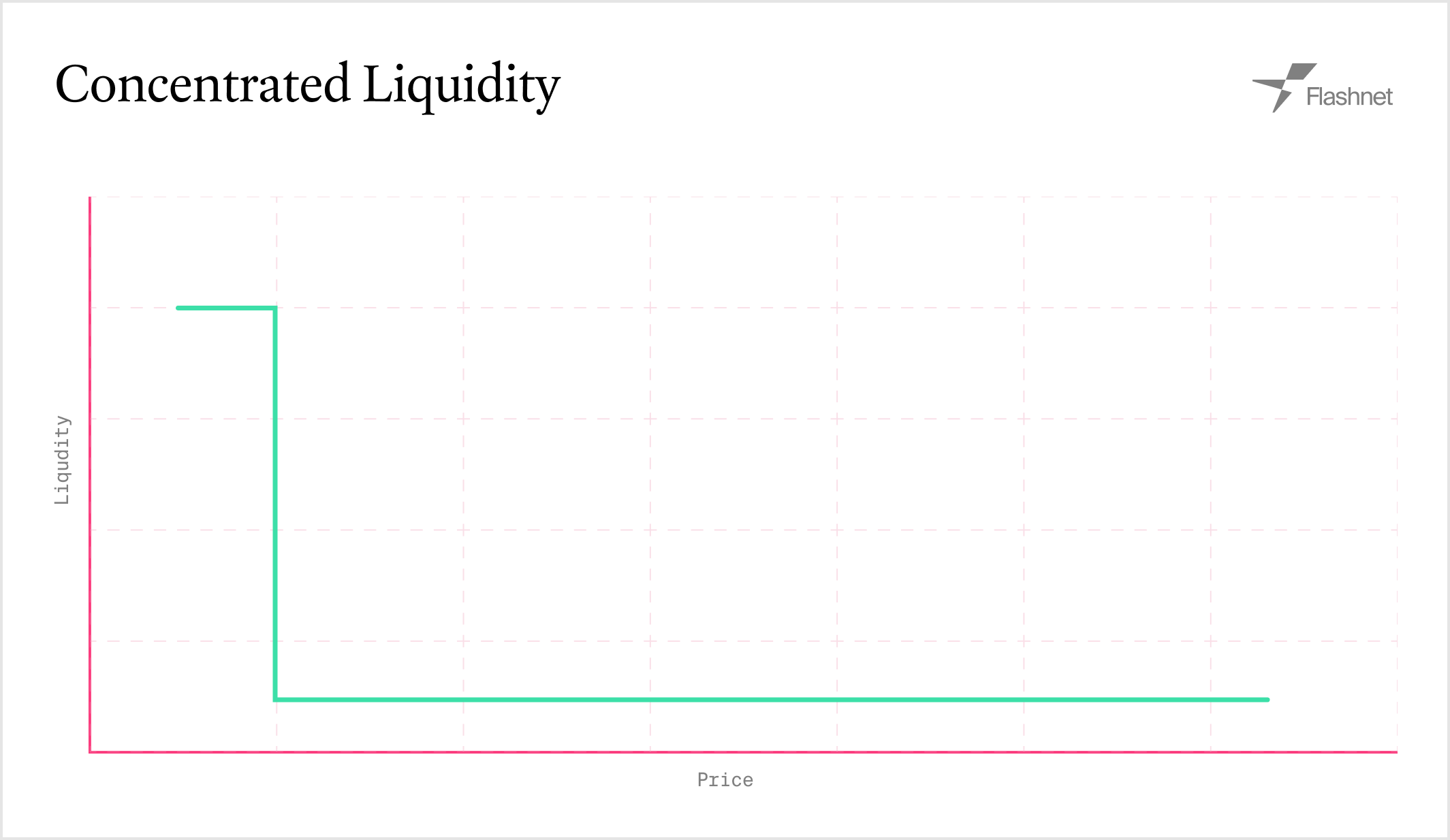The mathematical model follows concentrated liquidity formulas:
  • Liquidity Calculation:
    • Below range: L = (ΔA * sqrt(P_upper) * sqrt(P_lower)) / (sqrt(P_upper) - sqrt(P_lower))
    • Above range: L = ΔB / (sqrt(P_upper) - sqrt(P_lower))
    • Within range: L = min(L_A, L_B) where both assets may be required
  • Swap Execution: Swaps traverse tick boundaries, activating/deactivating liquidity as price moves
  • Fee Growth Tracking: Global and per-position fee growth is tracked for accurate fee distribution